Find the Vertex Form y=x^26x8 Complete the square for Tap for more steps Use the form , to find the values of , , and Consider the vertex form of a parabola Substitute the values of and into the formula Simplify the right side Tap for more steps Cancel the common factor of andX 2 2x 8 = 0 (x 2) (x 4) = 0 The graph intersects the xaxis at (2,0) and (4,0) Chapter 3 Passport to Advanced Math 185 14 A baseball is hit and flies into a field at aGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!
Graphing Quadratic Functions
Y=x^2-2x-8 vertex
Y=x^2-2x-8 vertex-Parabola, Finding the Vertex 21 Find the Vertex of y = x 2 2x8 Parabolas have a highest or a lowest point called the Vertex Our parabola opens up and accordingly has a lowest point (AKA absolute minimum) We know this even before plotting "y" because the coefficient of the first term, 1 , is positive (greater than zero)Find the vertex y = x2 4x Finding the Vertex of the Quadratic (from an equation in vertex form) Vertex Form makes finding the vertex easy Vertex Form y = a(x h)2 k The vertex is (h, k) Remember that the xvalue of the vertex is the OPPOSITE sign of what is in the equation



Graphing Parabolas Henri Picciotto Flip Ebook Pages 1 3 Anyflip Anyflip
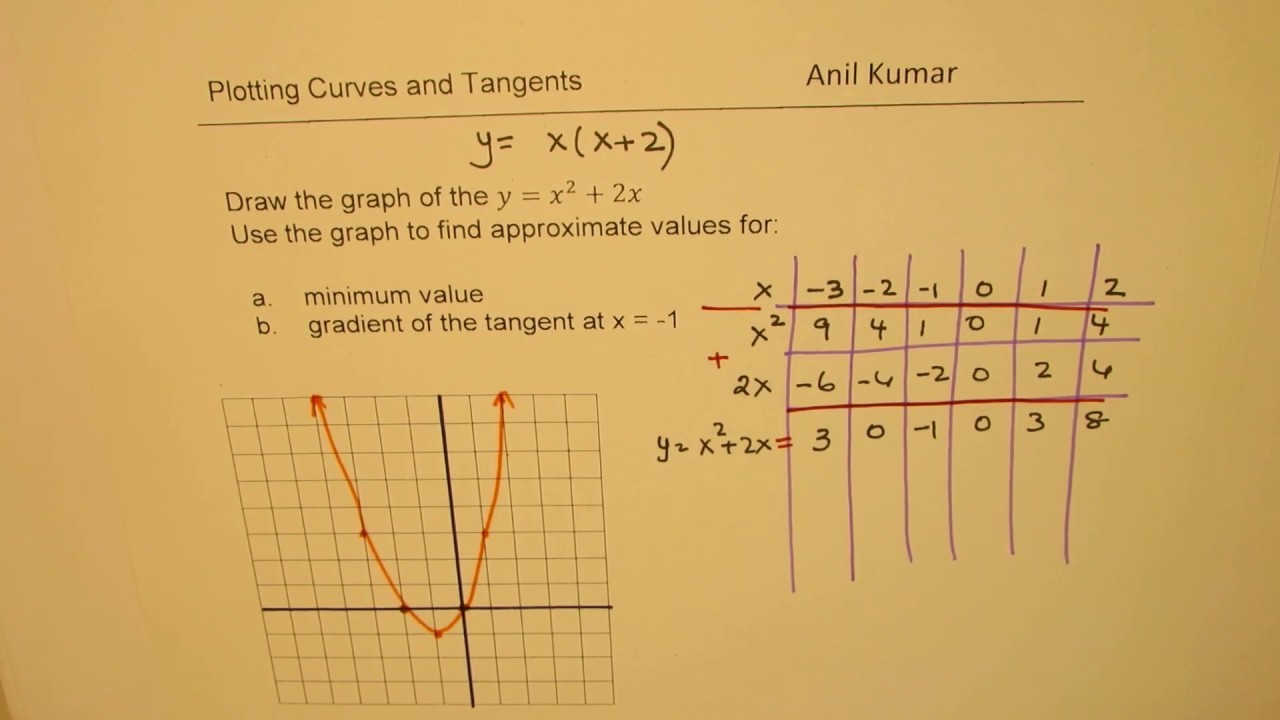
Free factor calculator Factor quadratic equations stepbystepThe maximum/minimum point (also known as the "vertex") can be found as follows The xcoordinate of this point is The a is the coefficient of the term and the b is the coefficient of the term In your equation, a = 1 and b = 2, so This is the xcoordinate of the vertexTo find the ycoordinate for the vertex we plug in h in the original equation k = a(h) 2 b(h) c Plot the points and graph the parabola Example 1) Graph y = x 2 2x 8 In this problem a = 1, b = 2 , and c = 8 Since "a" is positive we'll have a parabola that opens upward (is U shaped)
For any parabola, Ax2BxC, the x coordinate of the vertex is given by B/ (2A) In our case the x coordinate is Plugging into the parabola formula for x we can calculate the y coordinate y = 10 * 100 * 100 * 100 70 or y = 6000 Answer vertex (1,9) x intercepts (4,0) (2,0) Comment;Divide 0 0 by − 8 8 Multiply − 1 1 by 0 0 Add 8 8 and 0 0 Substitute the values of a a, d d, and e e into the vertex form a ( x d) 2 e a ( x d) 2 e Set y y equal to the new right side Use the vertex form, y = a(x−h)2 k y = a ( x h) 2 k, to determine the values of a a, h h, and k k
Divide 22\sqrt {y} by 2 The equation is now solved Swap sides so that all variable terms are on the left hand side Factor x^ {2}2x1 In general, when x^ {2}bxc is a perfect square, it can always be factored as \left (x\frac {b} {2}\right)^ {2} Take the square root ofDescription Learn to complete the square in order to write quadratic equations in vertex form Learning Objectives Stepbystep explanation y = x^2 2x 8 The axis of symmetry is h = b/2a h = 2/ (2*1) = 2/2 =1 x = 1 The x coordinate of the vertex is at the axis of symmetry To find the y value substitute into the function y




Converting A Quadratic Function From Standard Form To Vertex Form Completing The Square Youtube




Solved 1 For The Quadratic Function Y X2 2x 8 A F Chegg Com
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreFree functions vertex calculator find function's vertex stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy Vertex (1,1) There are two methods to solve this Method 1 Converting to Vertex Form Vertex form can be represented as y=(xh)^2k where the point (h,k) is the vertex To do that, we should complete the square y=x^22x2 First, we should try to change the last number in a way so we can factor the entire thing => we should aim for y=x^22x1 to make it look like




I Need To Get The Vertex Shape For A I Don T Know What I Am Doing Please Help Mathhomeworkhelp



Step To Draw Y X 2 4x 1and Find Solution To Quadratic Equation Y X 2 5x 4 Youtube
X^ {2}2x5=y Quadratic equations such as this one can be solved by completing the square In order to complete the square, the equation must first be in the form x^ {2}bx=c x^ {2}2x55=y5 Subtract 5 from both sides of the equation x^ {2}2x=y5 Subtracting 5 from itself leaves 0 x^ {2}2x1^ {2}=y51^ {2}Dallas Hogan 15 March, 21492 Input the xvalue of the vertex back into the quadratic to find the yvalue of the vertex 3 Input the vertex into the h and k values of the vertex form, which is y = a(x h)2 k 4 The a value is the coefficient in front of the x2 Convert to vertex form by completing the square



Solution Find The Vertex Of F X X 2 2x 8



How To Find The Domain And Range From Y X 2 2x 8 Quora
Parabola, Finding the Vertex 41 Find the Vertex of y = x 2 2x8 Parabolas have a highest or a lowest point called the Vertex Our parabola opens up and accordingly has a lowest point (AKA absolute minimum) We know this even before plotting "y" because the coefficient of the first term, 1 , is positive (greater than zero)Y = x2 − 2x − 8 y = x 2 2 x 8 Find the properties of the given parabola Tap for more steps Rewrite the equation in vertex form Tap for more steps Complete the square for x 2 − 2 x − 8 x 2 2 x 8 Tap for more steps Use the form a x 2 b xThe yintercept is at x=0 At x=0, y=0 so the yintercept is (0,0) The vertex is at the minimum (in this example) The 1st derivative is 2x2 2x2=0




Draw The Graph Of The Polynomial F X X 2 2x 8




File Y X 2 2x Svg Wikimedia Commons
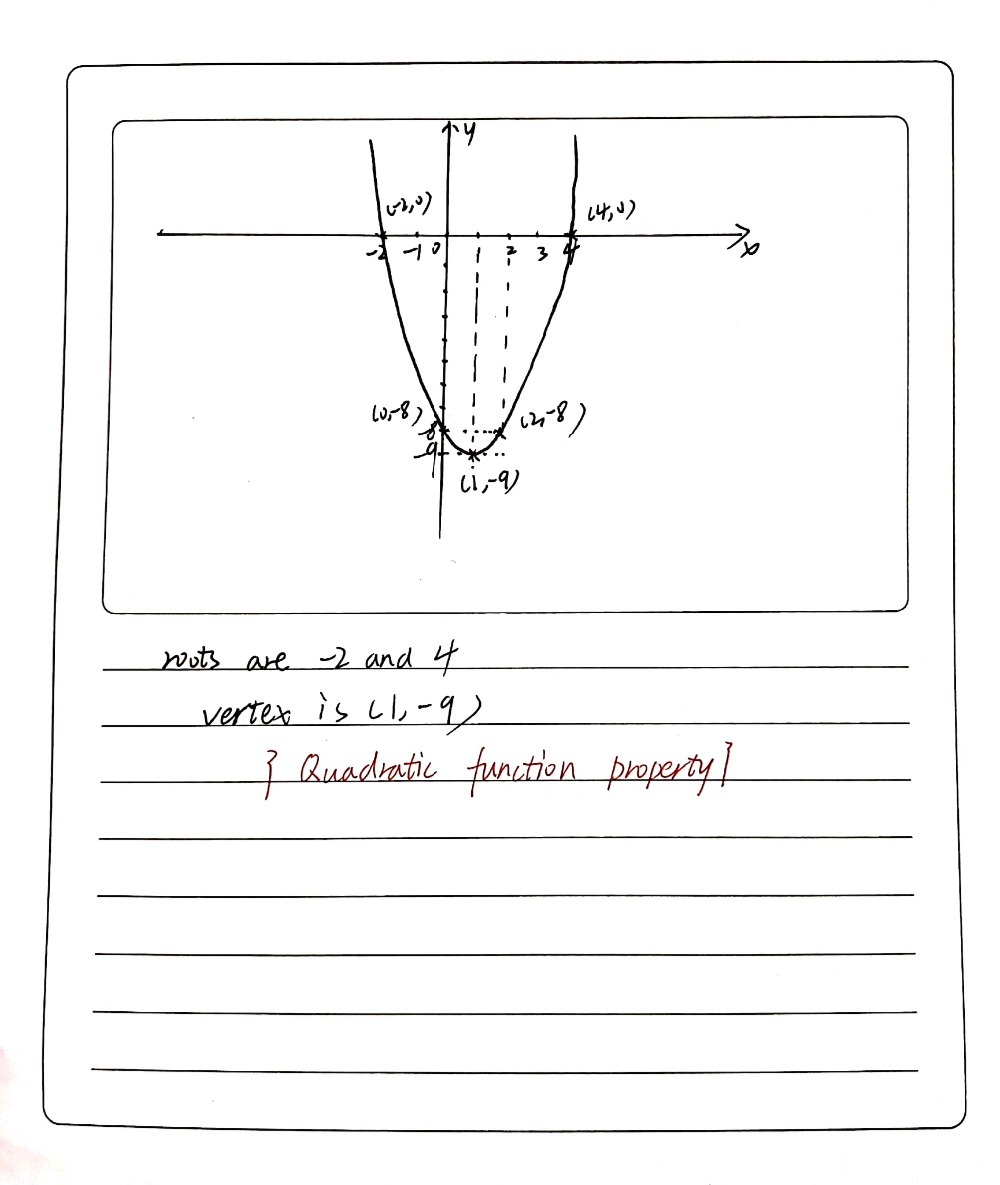
Y=x^22x8 (graph 300x0 pixels, x from 6 to 5, y from 10 to 10, y = 2x 8) according to the graph it is 4 for the x intercept also if you set y=0 we get the same answer 0=2x8Y = (x 2 2x 8) y = (x 2 2 ⋅ x ⋅1 1 218) y = ((x1) 29) y = (x1) 2 9 By comparing this with the vertex form of parabola, we get (h, k) ==> (1, 9) Example 6 y = (x1)(x3) Solution y = x 24x3 y = x 22 ⋅ x ⋅2 2 22 2 3 y = (x2) 243 y = (x2) 21 By comparing this with the vertex form of parabola, we getWhat Is The Axis Of Symmetry And Vertex For The Graph F X X 2 2x 8 Socratic For more information and source, Solution 3 The Graph Of Y X 2 2x 8 Intersects The X Axis At 1 2 And 4 2 2 And 4 3 2 And 4 4 2 And 4 Please Show Steps For more information and source,




Y X 2 2x 8 Xy Vertex Max Or Min Axis Of Symmetry Do Now 4 From Classwork Ppt Download



Search Q Vertex Form Tbm Isch
Write the equation in vertex form {eq}y=x^22x8 {/eq} Vertex Form of a Parabola The vertex of a parabola is a point where the parabola has a maximum or a minimum valueAlgebra Find the Vertex Form y=x^22x8 y = x2 − 2x − 8 y = x 2 2 x 8 Complete the square for x2 −2x−8 x 2 2 x 8 Tap for more steps Use the form a x 2 b x c a x 2 b x c, to find the values of a a, b b, and c c a = 1, b = − 2, c = − 8 a = 1, b = 2, c =Found 2 solutions by checkley75, jim_thompson5910 Answer by checkley75 (3666) ( Show Source ) You can put this solution on YOUR website!




Identify Quad Parts Projectile Motion 1 Docx Motion Physics Physics



How To Draw Y 2 X 2
Solved by pluggable solver Completing the Square to Get a Quadratic into Vertex Form Start with the given equation Subtract from both sides Factor out the leading coefficient Take half of the x coefficient to get (ie ) Now square to get (ie ) Now add andParabola, Finding the Vertex 31 Find the Vertex of y = x 22x8 Parabolas have a highest or a lowest point called the Vertex Our parabola opens up and accordingly has a lowest point (AKA absolute minimum) We know this even before plotting "y" because the coefficient of the first term, 1 , is positive (greater than zero)Complete the square y = 2x^2 3x 7 = 2 (x^2 3/2 x) 7 = 2 (x^2 3/2 x 9/16) 7 2 (9/16) = 2 (x 3/4)^2 7 9/8 = 2 (x 3/4)^2 56/8 9/8 = 2




Plot A Graph For The Equation Y X 2 4x 1



Why Is It In Vertex Form Of Quadratic Function Y A X H 2 K Getting Value Of H Is Opposite To Its Value Quora
Subtract y from both sides Subtract y from both sides x^ {2}2x8y=0 x 2 2 x − 8 − y = 0 All equations of the form ax^ {2}bxc=0 can be solved using the quadratic formula \frac {b±\sqrt {b^ {2}4ac}} {2a} The quadratic formula gives two solutions,Vertex Form Equation & Functions Just as y = mx b is a useful format for graphing linear functions, y = a(x h)^2 k is a useful format for graphing quadratic functionsParabola, Finding the Vertex 71 Find the Vertex of y = x 22x8 Parabolas have a highest or a lowest point called the Vertex Our parabola opens up and accordingly has a lowest point (AKA absolute minimum) We know this even before plotting "y" because the coefficient of the first term, 1 , is positive (greater than zero)



Math Spoken Here Classes Quadratic Equations 3



5 3 Vertex Form Of Quadratic Functions Translating
This problem has been solved!The axis of symmetry and the vertex of this quadratic function are calculated by hand The results are compared with the results obtained by using a graphing To change the expression (x2 2x) into a perfect square trinomial add (half the x coefficient)² to each side of the expression Here x coefficient = 2 So, (half the x coefficient)2 = (2/2)2 = 1 Add and subtract 1 to the expression The vertex form of the parabola with vertex (h, k) and axis of symmetry x = h is y = a (x h)2 k




How To Analyze A Parabola 6 Steps With Pictures Wikihow



How Do I Find The Vertex Of F X X 2 8x 7 Socratic
Y X 2 2x 8 Parabola Solution For The Quadratic Function F X X 2 2x 8 Find A The Axis Of Symmetry And The Vertex B The X Intercepts And Y Intercepts C The Domain And Range D For more information and source, see on this link httpsSo the xcoordinate of the vertex is Lets plug this into the equation to find the ycoordinate of the vertex Lets evaluate Start with the given polynomial Plug in Raise 1 to the second power to get 1 Multiply 2 by 1 to get 2 Negate any negatives Now combine like terms So the vertex is (1,9)See the answer Find the xintercept (s) and the coordinates of the vertex for the parabola y=x^22x8 If there is more than one xintercept, separate them with commas Show transcribed image text




F X X2 2x 8 Novocom Top



Http Www Manhassetschools Org Cms Lib8 Ny Centricity Domain 710 Group work 59 63 solutions Pdf
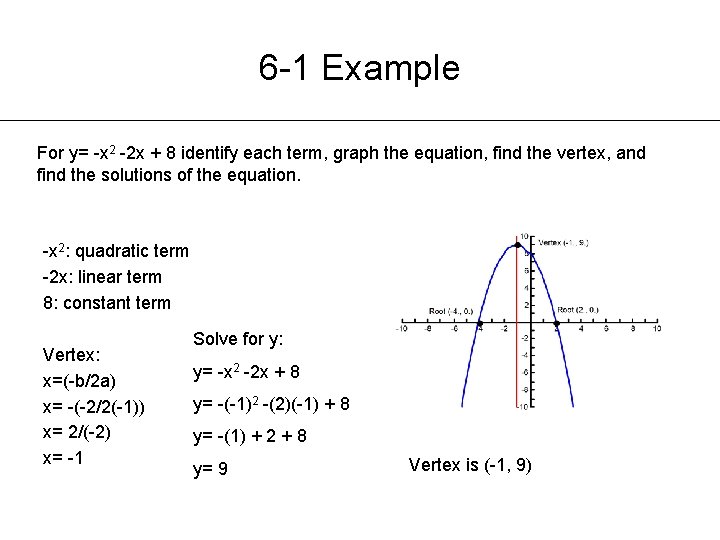
a the vertex b the axis of symmetry c the intercepts d the domain e the range f the interval where the function is increasing, and g the interval where the function is decreasing h Graph the function y= x^22x8Steps for Completing the Square View solution steps Steps Using the Quadratic Formula y = \left ( x4 \right) \left ( x2 \right) y = ( x 4) ( x − 2) Use the distributive property to multiply x4 by x2 and combine like terms Use the distributive property to multiply x the xcoordinate of the vertex is x = b/(2a) For the problem y = x 2 2x 8, a = 1, b = 2, and c = 8, so, the xcoordinate of the vertex is x = 2/2 or 1 Substituting this value back into the equation y = (1) 2 2(1) 8 = 9 Putting this together, the vertex is (1, 9)



Solution Find The Vertex The Y Intercept And The X Intercept And Graph The Function Y X2 2x 8 It 39 S X Squared



Quadratic Functions
But the equation for a parabola can also be written in "vertex form" y = a ( x − h) 2 k In this equation, the vertex of the parabola is the point ( h, k) You can see how this relates to the standard equation by multiplying it out y = a ( x − h) ( x − h) k y = a x 2 − 2 a h x a h 2 k This means that in the standard form, y13 At what points the graph of y = x2 2x 8 cuts the x Answer (c) a) (2,0) and (0,0) b) (0, 0) and (2, 0) c) (2, 0) and (4, 0) d) (4,0) and (2, 0) axis?Y = x2 − 2x − 8 y = x 2 2 x 8 Rewrite the equation in vertex form Tap for more steps Complete the square for x 2 − 2 x − 8 x 2 2 x 8 Tap for more steps Use the form a x 2 b x c a x 2 b x c, to find the values of a a, b b, and c c a = 1, b = − 2, c = − 8 a = 1, b = 2, c = 8 Consider the vertex form of a parabola



3



Graphs Of Functions Y X2 Y 2x2 And Y 2x2 In Purple Red And Blue Respectively
A) y = 2x 2 12x 16 B) y = 2x (x 6) 16 C) y = 2 (x 3) 2 (2) D) y = (x 2) (2x 8) Answer If you know the vertex form of an equation y = a (x h) 2 k then you will notice that only answer C is in that form Go to next Question Try the free Mathway calculator and problem solver below to practice various math topics Vertex Form Of A Quadratic The vertex form of a quadratic is given by y = a(x – h) 2 k, where (h, k) is the vertexThe "a" in the vertex form is the same "a" as in y = ax 2 bx c (that is, both a's have exactly the same value) The sign on "a" tells you whether the quadratic opens up or opens downThink of it this way A positive "a" draws a smiley, and a negative The vertex of the parabola has coordinates (1, 9) ie (b/2a,D/4a), where D =b 2 4ac (iv) The polynomial f(x) = x 2 2x 8 = (x 4) (x 2) is factorizable into two distinct linear factors (x 4) and (x 2) So, the parabola cuts Xaxis at two distinct points (4, 0) and (2, 0) the xcoordinates of these points are zeros of f(x)



View Question What Is The Vertex Of The Equation Y X 2 2x 8




Graph The Parabola And Give Its Vertex Axis X Intercepts And Y Intercept Y 2x 2 8x 16 Study Com




Solve By Completing The Square X 2 2x 8 0 Solving Quadratic Equations Youtube



Quadratic Functions



Zmsmio0vpjrczm



Chapter 6 Exploring Quadratic Functions And Inequalities By



Graph The Equation Y X2 2x 8 On The Accompanying S Gauthmath



Answered A Quadratic Function F Is Given F X Bartleby



2



What Are The Coordinates Of The Vertex For F X X 4x 10 Quora



Practice 1 2 Graphing In Vertex Form And Intercept Form




Use The Drawing Tool S To Form The Correct Answer On The Provided Graph Consider The Function Brainly Com




Quadratic Function




Use The Graph Of The Function Y X2 2x 8 To Determine The Solutions Of The Quadratic Brainly Com




Finding Features Of Quadratic Functions Video Khan Academy




Write The Equation In Vertex Form Y X 2 2x 8 Study Com



Ch 7 8
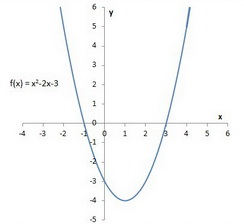



How Do I Convert The Equation F X X 2 2x 3 To Vertex Form Socratic




3 Vertex Form



Solution Use The Graph Of Y X 2 2x 8 Does This Function Have A Maximum And Minimum And If So What Are They




Vertex Axis Of Symmetry Of A Parabola Video Khan Academy



Q Tbn And9gcrp9hpi7emwokn0e2fajh3aom0rmz7yizyhaftxq5127se4oc4j Usqp Cau




How To Draw Y 2 X 2




Answered Work All Problems On Your Own Paper Bartleby



Graphing Quadratic Functions
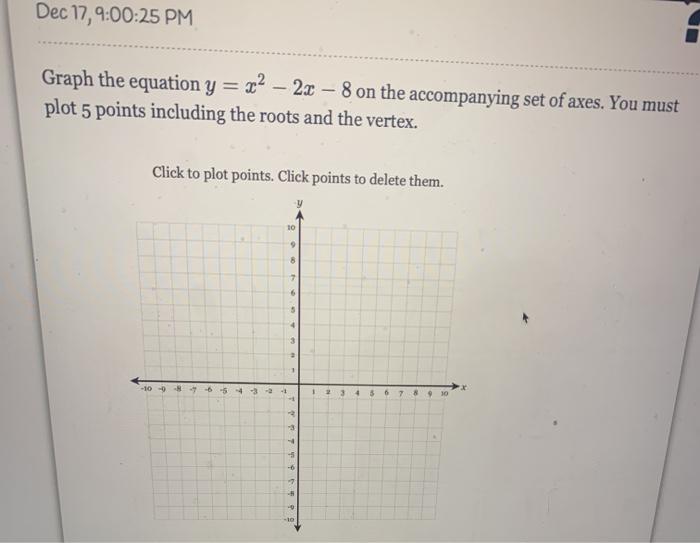



Solved Dec 17 9 00 25 Pm Graph The Equation Y X2 2x Chegg Com
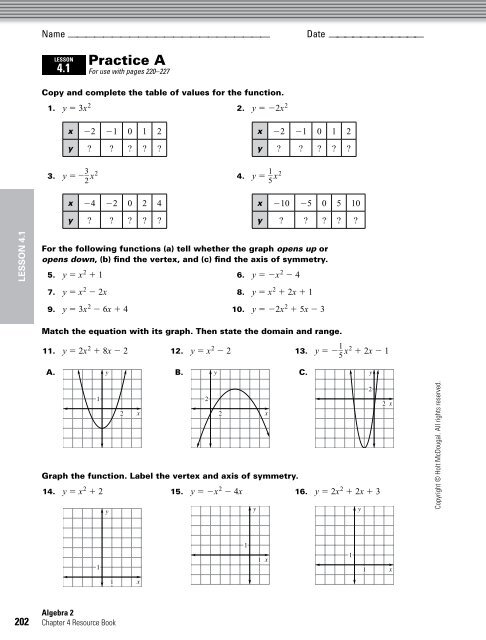



Practice Mathnmind



Solution What Is The Vertex Form Of F X X 2 2x 5



Graphing Parabolas Henri Picciotto Flip Ebook Pages 1 3 Anyflip Anyflip




2 02 Quadratic Equations



2



Draw The Graph Of The Polynomial F X X 2 2x 8 Sarthaks Econnect Largest Online Education Community




A Portion Of The Graph Of F X X2 2x 8 Is Shown Which Of The Following Describes All Brainly Com
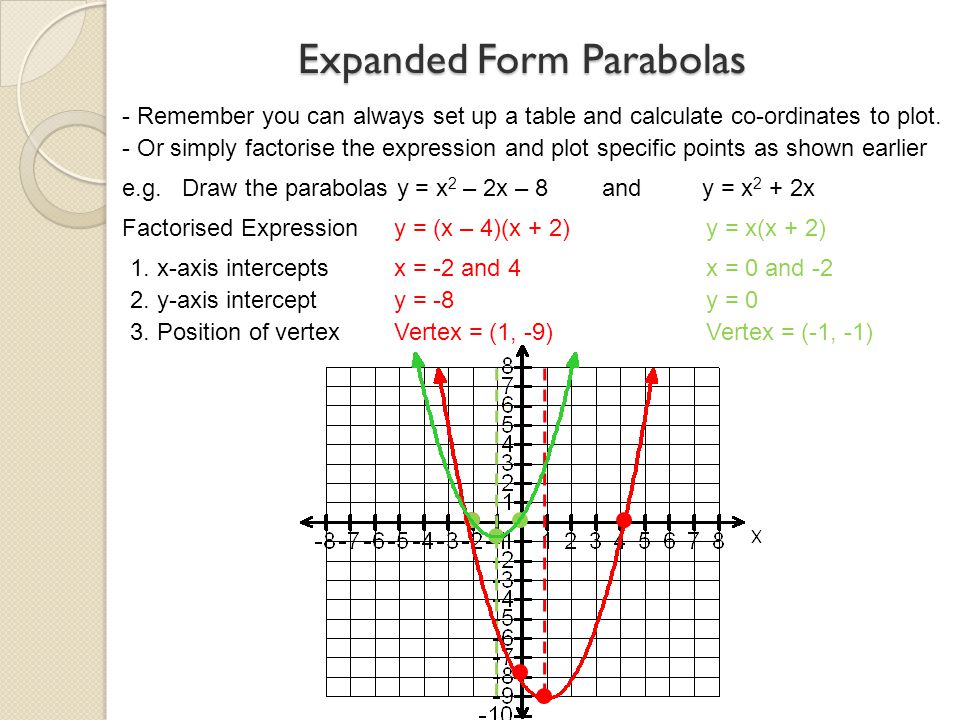



Algebra Graphs Plotting Points To Draw Straight Line Graphs We Can Use A Rule To Find And Plot Co Ordinates E G Complete The Tables Below To Find Ppt Download



2




Graphing Parabolas




2 02 Quadratic Equations



How Do You Find The Vertex Of The Parabola Y 2x 2 8x 7 Socratic



Http Www Tippcityschools Com Cms Lib6 Oh Centricity Domain 91 Quadratics review ws solutions Pdf




Algebra 1 Find The Vertex Of Y X 2 2x 8 Using A Graphing Calculator Youtube



Http Www Tatecountyschools Org Userfiles 157 Classes 850 A3 7 6 solving quadratic equations Pdf Id



Q Tbn And9gctwl8ksal48ks9fvcggchq7ifw Mt5nzxx1 0ivsjobxia io Usqp Cau
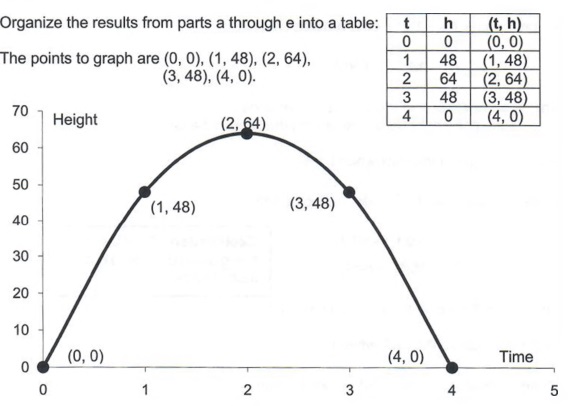



Graph Graph Equations And Equation Systems With Step By Step Math Problem Solver




Ppt Chapter 6 Exploring Quadratic Functions And Inequalities Powerpoint Presentation Id




Transformations Of Quadratic Functions College Algebra




Draw The Graph Of The Polynomial F X X 2 2x 8
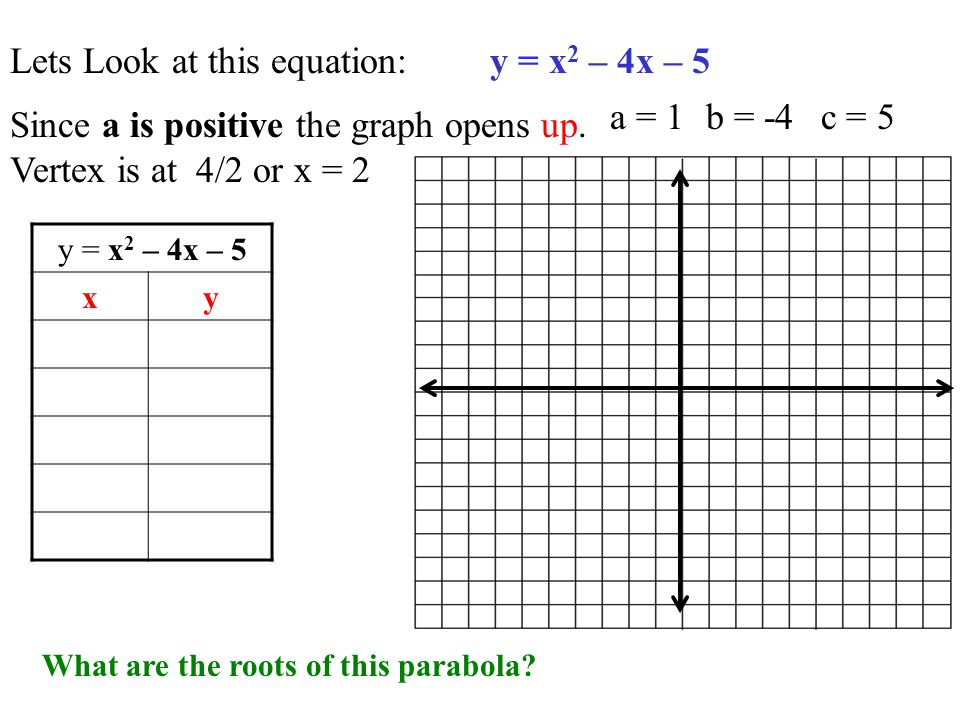



Y X 2 2x 8 Xy Vertex Max Or Min Axis Of Symmetry Do Now 4 From Classwork Ppt Download




Write The Quadratic Function In The Standard Form Y Chegg Com
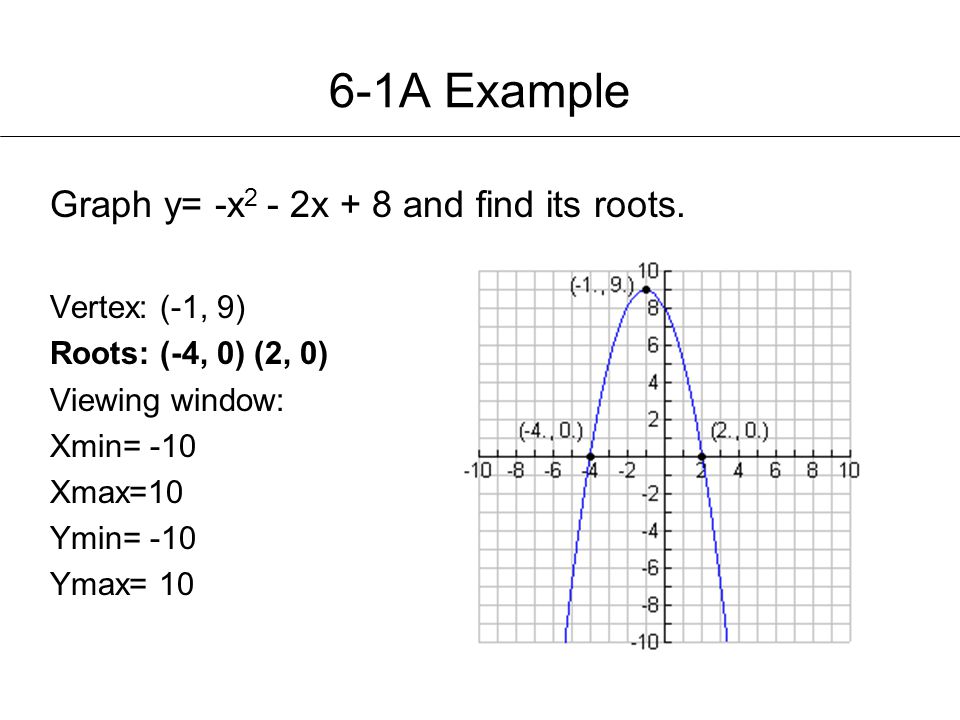



Chapter 6 Exploring Quadratic Functions And Inequalities Ppt Video Online Download
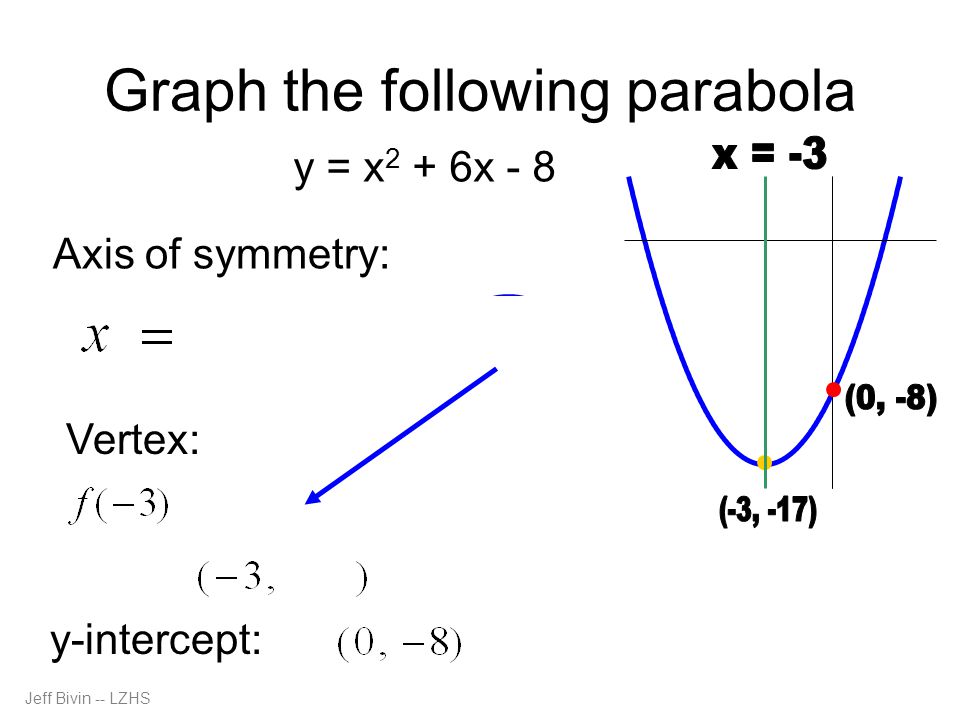



Graphing Parabolas Using The Vertex Axis Of Symmetry Y Intercept By Jeffrey Bivin Lake Zurich High School Last Updated October Ppt Download




Excelsior Math 8 Unit 7 Flashcards Quizlet



Www Lcps Org Cms Lib Va Centricity Domain Graphing quadratic key Pdf



2
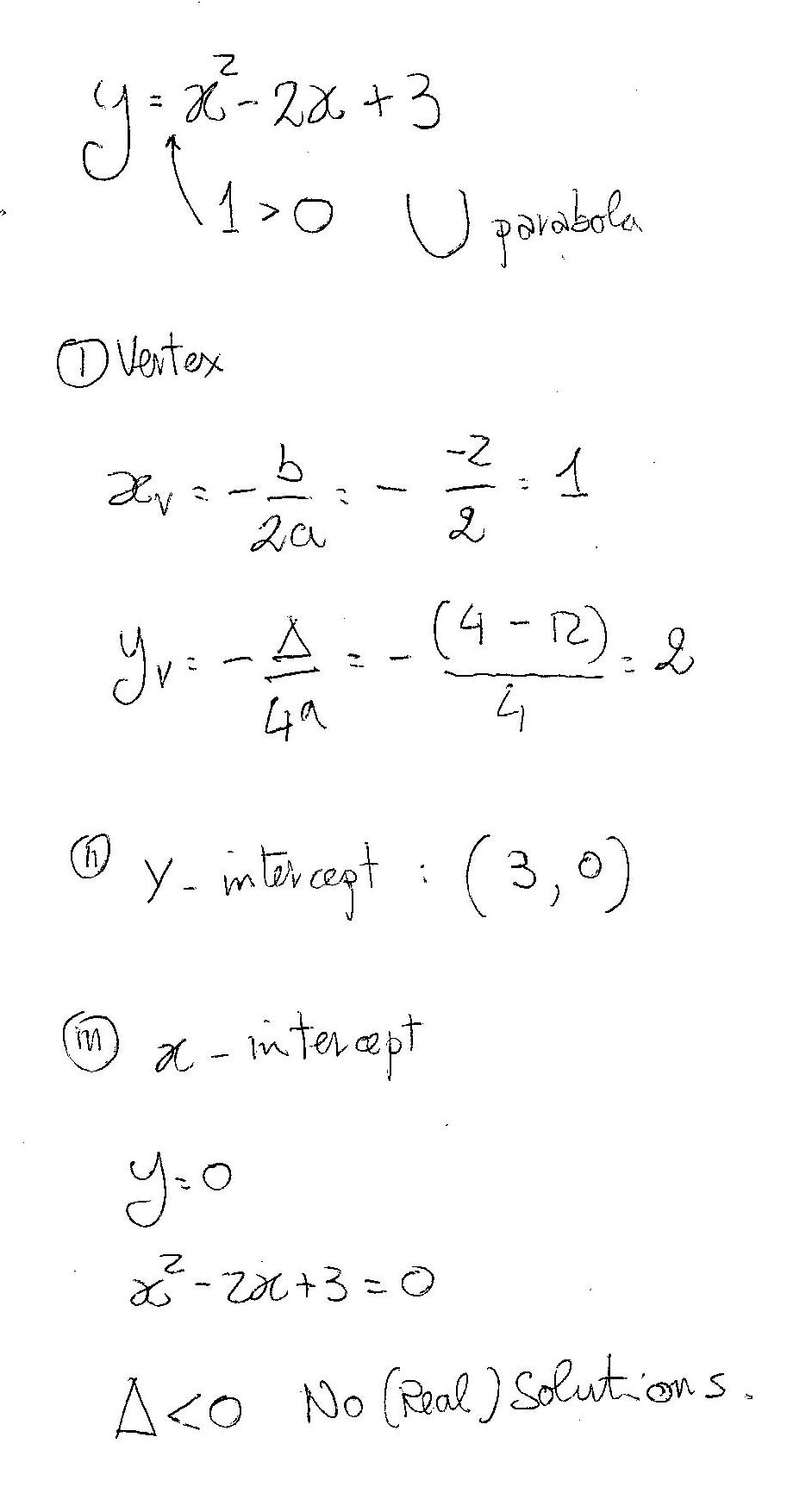



How Do You Graph Y X 2 2x 3 Socratic



Quadratic Functions



What Is The Axis Of Symmetry And Vertex For The Graph F X X 2 2x 8 Socratic




6 For The Quadratic Function F X X2 2x 8 A Chegg Com




For The Function F X X 2 2x 8 Find The Chegg Com
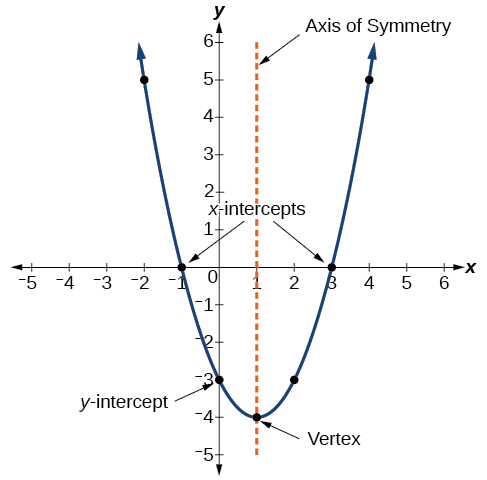



5 1 Quadratic Functions Mathematics Libretexts




Vertex Intercept And Standard Form Ck 12 Foundation



Solution In A Graph Of Y X 2 2x 9 How Would One Find The Vertex Of This Graph Your Help Would Be Sincerely Appreciated
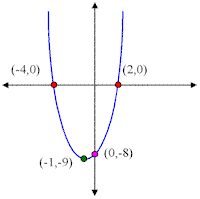



Parabolas
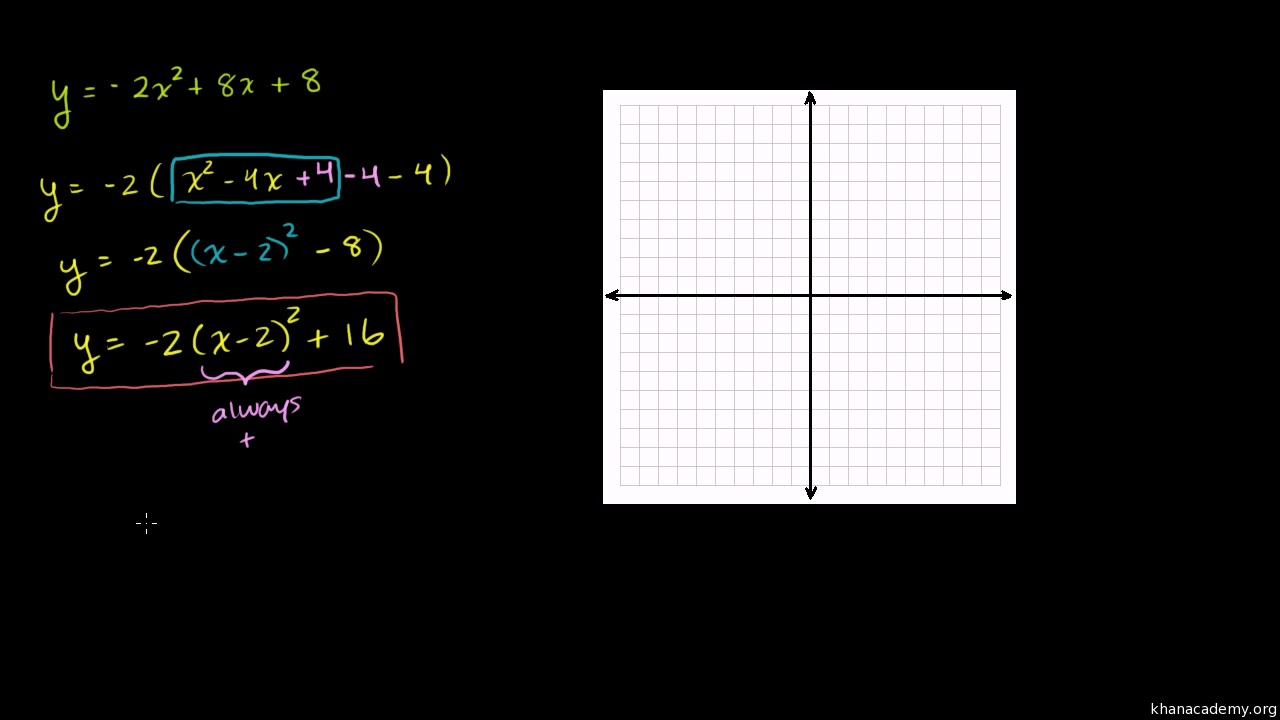



Vertex Axis Of Symmetry Of A Parabola Video Khan Academy
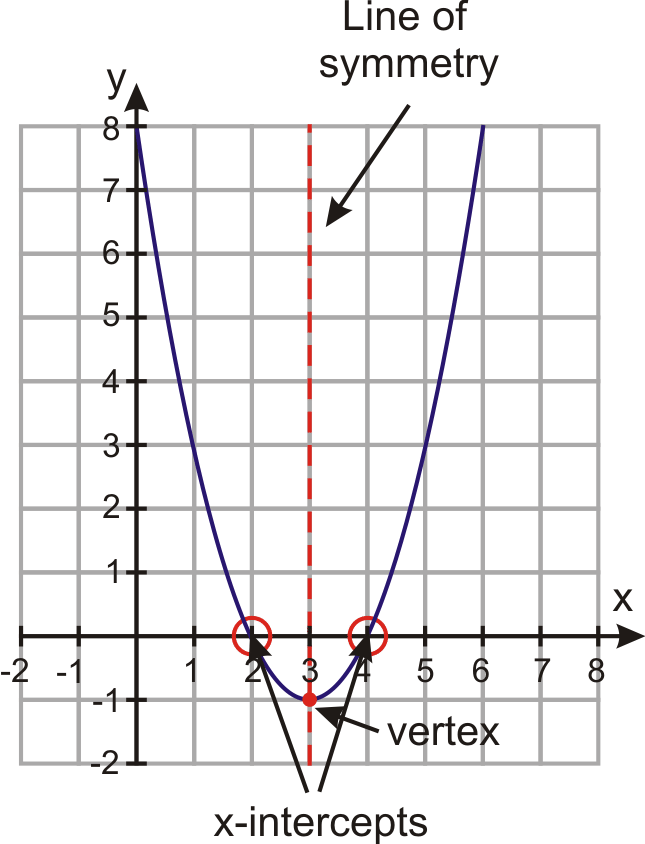



Graphs Of Quadratic Functions In Intercept Form Read Algebra Ck 12 Foundation



Graphing Quadratic Functions
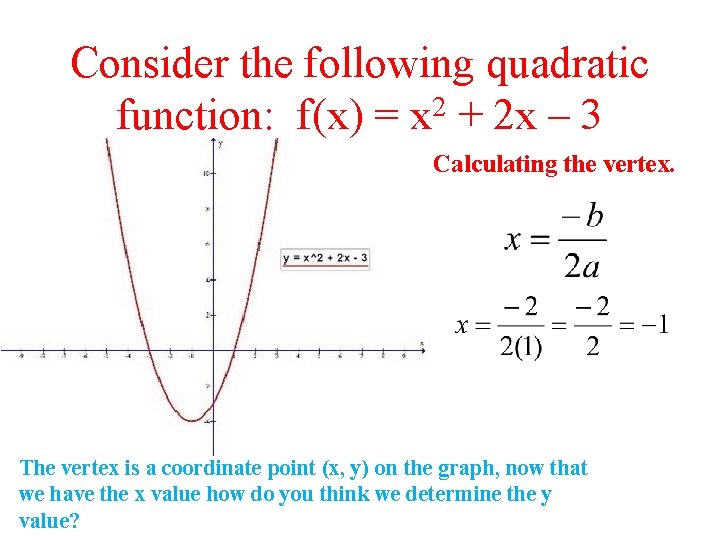



Quadratic Functions Ticket In The Door Lesson Essential




Graphing Parabolas




7 Graph The Parabola Y X2 2x 8 On The Grid Provid Gauthmath



How Do You Sketch The Graph Of Y X 2 8 And Describe The Transformation Socratic




5 Write The Equation Of The Parabola In Vertex Form Chegg Com




Find Factored Form And Vertex Of F X X 2 2x 8 Youtube
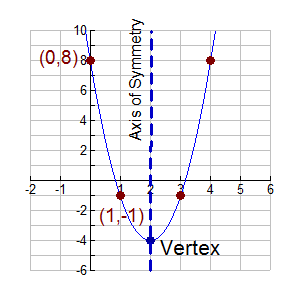



Vertex Form Of Quadratic Equation Mathbitsnotebook Ccss Math



Solution For The Quadratic Function F X X 2 2x 8 Find A The Axis Of Symmetry And The Vertex B The X Intercepts And Y Intercepts C The Domain And Range D
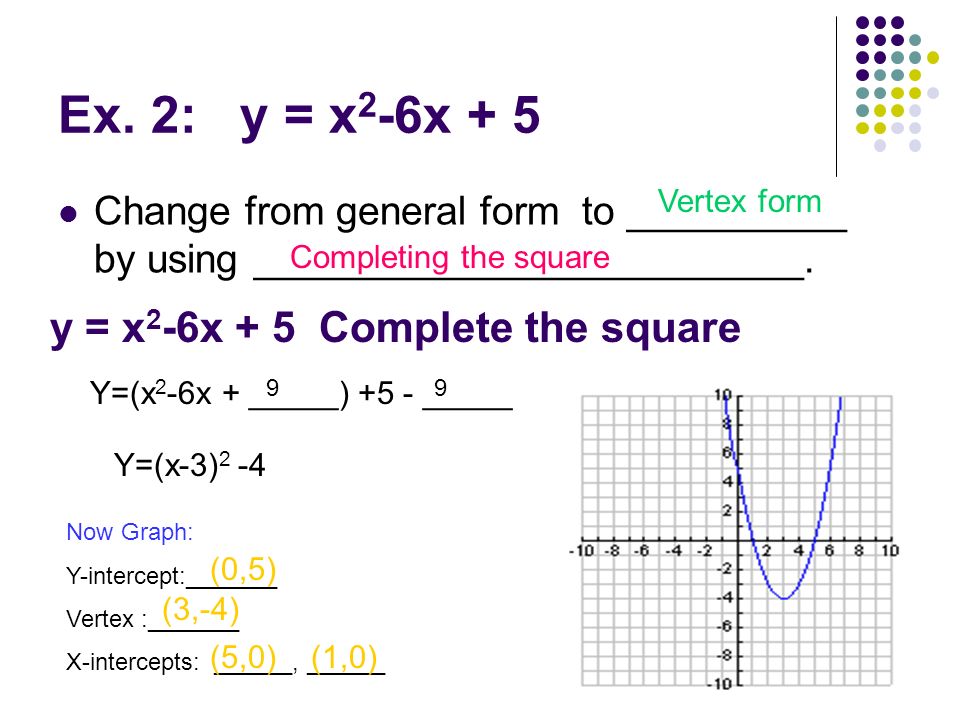



Warm Up Find The Vertex The Roots Or The Y Intercept Of The Following Forms 1 F X X 4 F X 2 X 3 X 4 3 F X X 2 2x 15 Answers Ppt Download
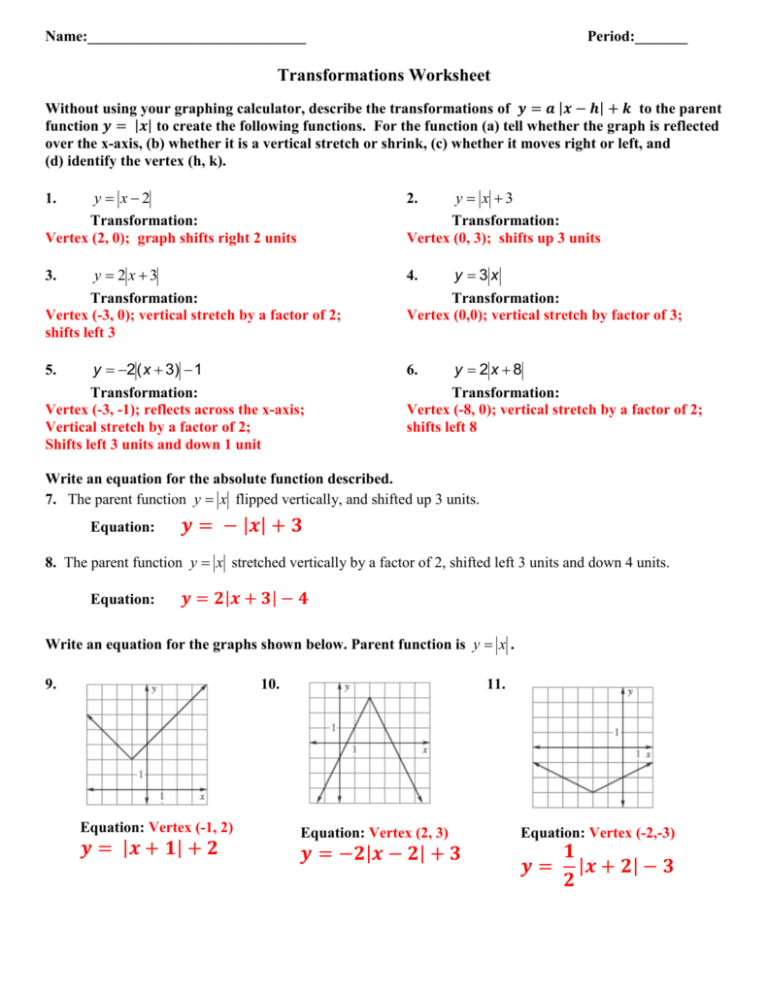



Absolute Value Transformations




Vertex Form Vertex Form Vertex Form Is Another



2
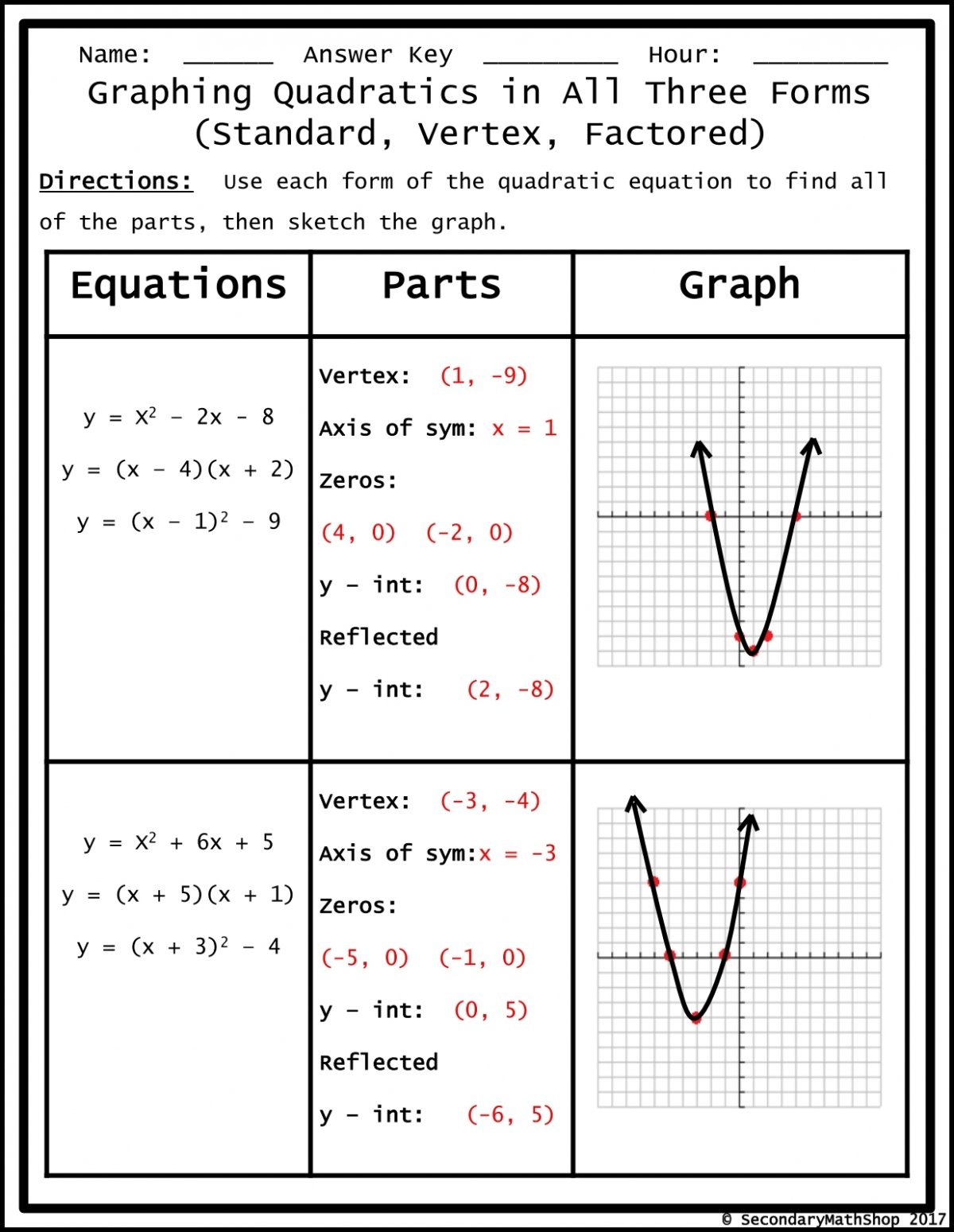



Quadratic Eq Graph Parabola Symmetry
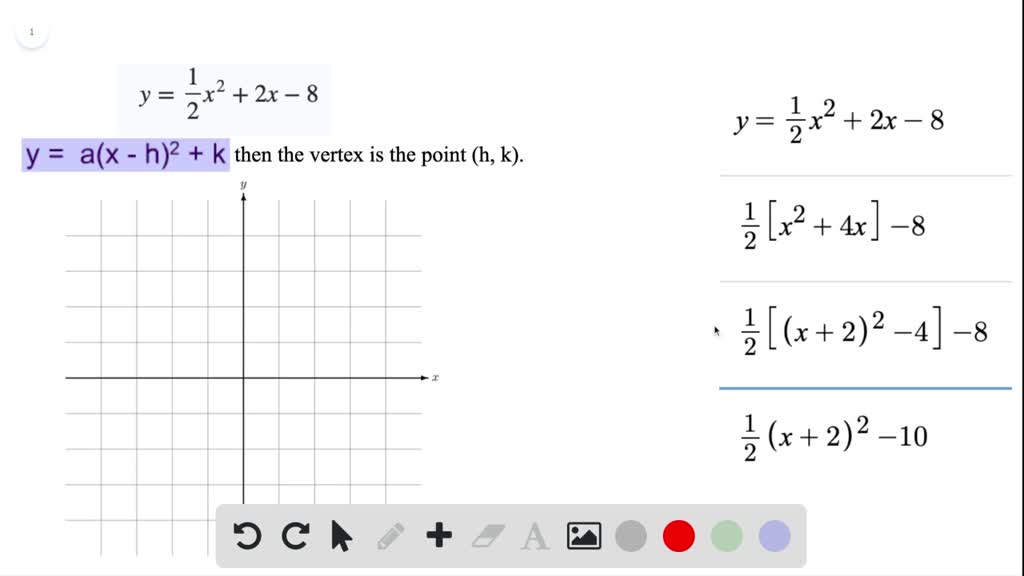



Solved Graph Each Function Label The Vertex And



Www D105 Net Cms Lib Il Centricity Domain 610 Vertex practice worksheet answers Pdf



0 件のコメント:
コメントを投稿