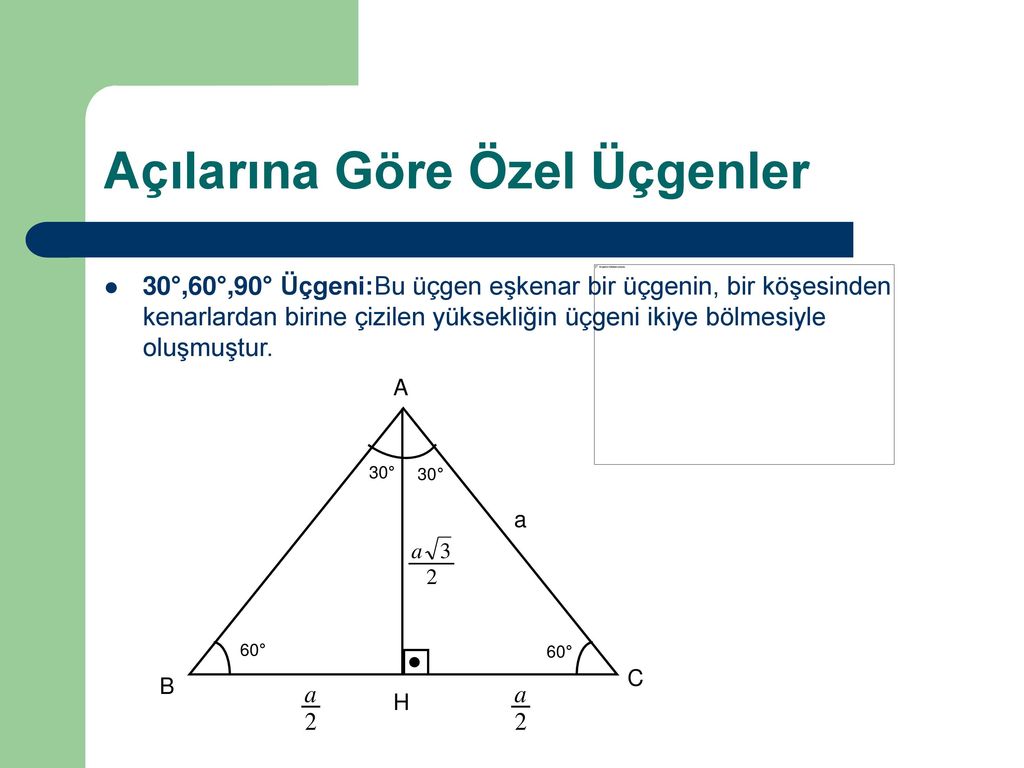
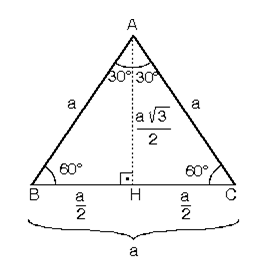
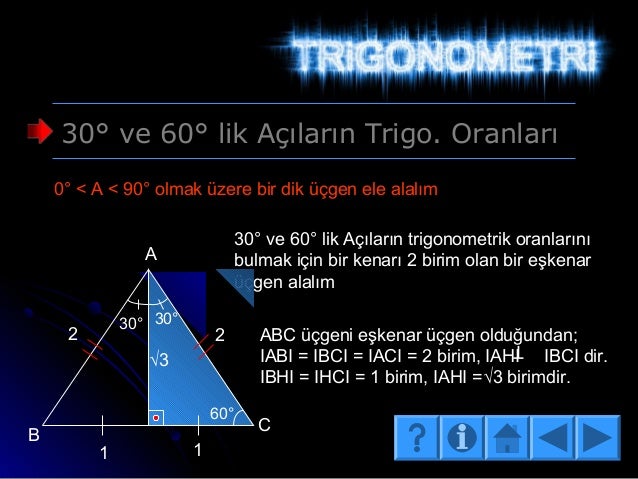
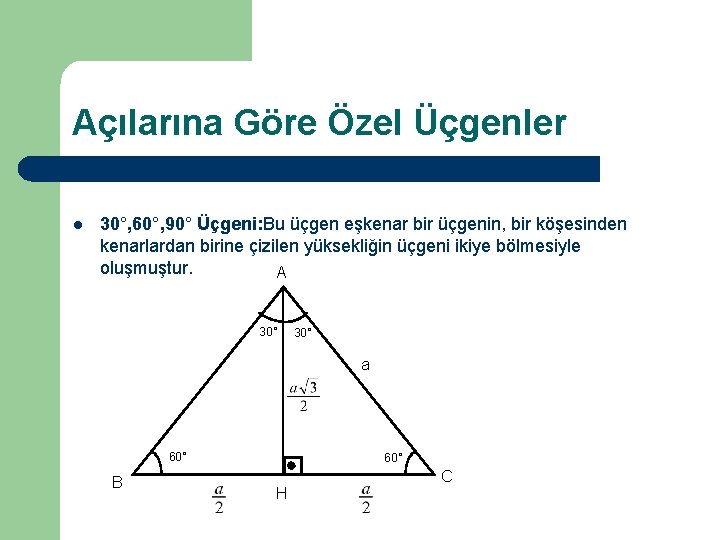
4 (30° – 60° – 90°) Üçgeni ABC eşkenar üçgeni yükseklikle ikiye bölündüğünde ABH ve ACH (30° 60° 90°) üçgenleri elde edilir AB = AC = a BH = HC = pisagordan (30° 60° 90°) dik üçgeninde; üçgeni aynı zamanda kenarlarını da etkilemektedir Böylece açıların karşısındaki kenar ile beraber diğer kenarları üzerinden belli bir bağıntı bulunur Bu bağlantı sayesinde hem kenarlar hem de açılar kolay bir şekilde bulunabilmektedir 30 60 90 Üçgeni Nedir? 30 60 90 üçgeninin özel üçgenler arasında yer almasının asıl nedeni iç açıları birbirine eşit olan ve her biri 60° olan ABC eşkenar üçgeninden 2 adet dik üçgen elde edilmesidir ABC eşkenar üçgeni A açısından çizilen yükseklikle ikiye bölünür ve H noktası ile belirlenir

45 45 90 Ucgeni Ve Ozellikleri Not Bu
30 60 90 üçgeni kenarları
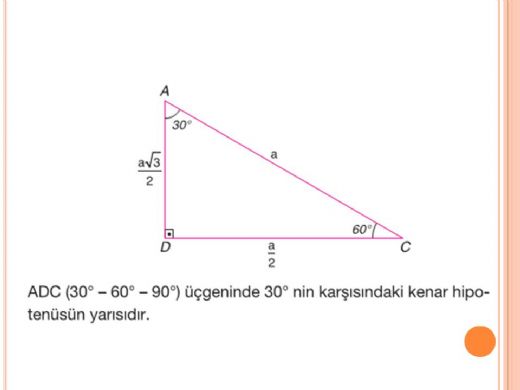
30 60 90 üçgeni kenarları- 30 60 90 ÜÇgenİ sorulari ABC bir dik üçgendir AB kenarı BC kenarına diktir m (BCA) = 30 derecedir AC kenarı uzunluğu ise 8 cm dir Bu verilere göre BC kenar Yukarıdaki şekildeki ABD üçgeni bir 30 60 90 üçgenidir 30 60 90 üçgeninde 90°'lik açının karşısındaki kenarın (hipotenüsün) uzunluğu 30°'lik açının karşısındaki kenarın uzunluğunun 2 katı ve 60°'lik açının karşısındaki kenarın uzunluğu da




30 60 90 Ucgeni Ibrahim Hocca
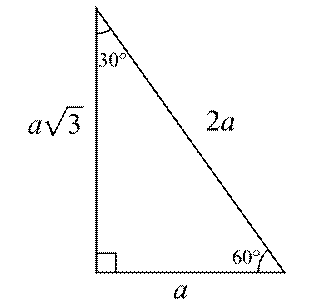
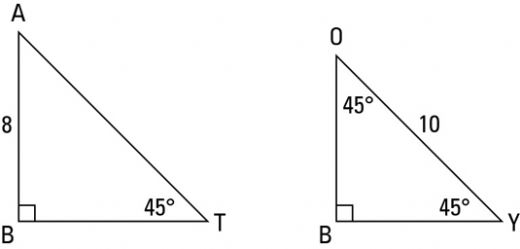
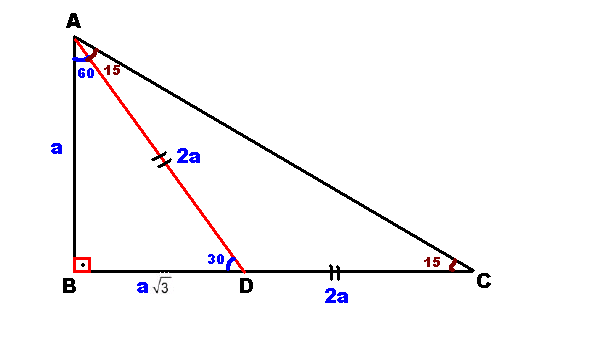
30 60 90 üçgeninde 30 derecenin karşısındaki kenar a birim, 60 derecenin karşısında a√3 ve 90 derecenin karşısında 2a birim olur Bu oranlar çok önemlidir Birçok trigonometrik oran bu oranlardan elde edilirBurada 75 dereceyi 15'e 60 olarak böldük Bir tarafta 0 ikizkenar üçgeni, diğer tarafta da özel üçgeni oluştu Buna göre kenarları yazdık 90'ın karşısını da pisagordan bulursunuz artık İyi günler üçgeni bir ikizkenar dik üçgendir Üçgenin dik kenarları birbirine eşit ve hipotenüsü dik kenarların katıdır Oran aşağıdaki gibidir İspatı ise çok basittir Bir dik kenara 1 cm denilirse, ikizkenarlıktan dolayı diğer dik kenar da 1 cm olmak zorundadır Pisagor Teoremi'nden de hipotenüs çıkar
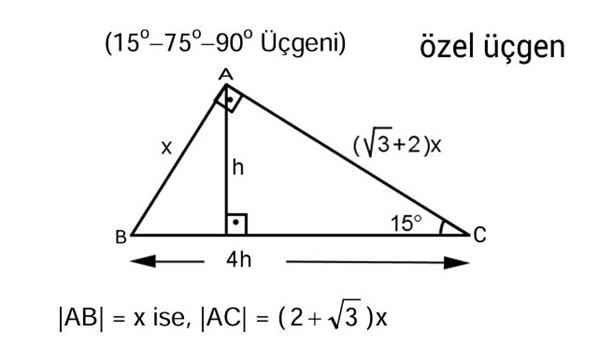
Açıları olan bir dik üçgende hipotenüs, 30°'nin karşısındaki kenar ve 60°'nin karşısındaki kenar arasında sırasıyla aşağıdaki oran vardır 30°'nin karşısındaki kenarın katıdır İspatı ise eşkenar üçgen vasıtasıyla yapılır Kenarları 2 cm olan bir 75 dereceyi 1560 derece olacak şekilde ayıran bir kenar çizip karşı dik kenar ile birleştirirsek, bir tarafta ikizkenar üçgen diğer tarafta üçgeni oluşur ve kenar uzunlukları arasındaki bağıntı ezberlenmemiş olur dik kenarlar arasındaki bağıntıyı hatırlayacak olursak, 15 in karşısındaki kenar "a" ise 75 in Üçgeni Bir dik üçgende dar açılardan biri 30 ise, 30 derecelik açının karşısındaki kenar hipotenüsün yarısında eşittir 60 derecelik açının karşısındaki kenarın uzunluğu da 30 derecelik açı karşısındaki kenarın katına eşittir
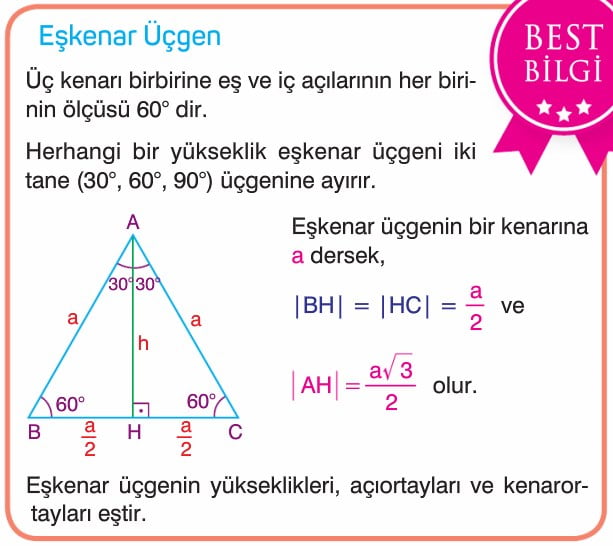
Eşkenar Üçgen Konu Anlatımı Üç kenarı birbirine eş ve iç açılarının her birinin ölçüsü 60°'dirHerhangi bir yükseklik eşkenar üçgeni iki tane üçgenine ayırırEşkenar üçgenin yükseklikleri, açıortayları ve kenarortayları eşittir Şimdi Eşkenar üçgenlerle ilgili bilmenHipotenüs Uzunluğu 108,1666 birim Komşu Kenar Uzunluğu 90 birim Karşı Kenar Uzunluğu 60,0001 birim Yukarıdaki ölçüleri bildiğimizi varsayalım Aşağıdaki α ve β açısının matematiksel hesaplama formülü nedir bununla alakalı bir bilgi paylaşılmam 0042(30° – 60° – 90°) Üçgeni ABC eşkenar üçgeni yükseklikle ikiye bölündüğünde ABC eşkenar üçgeni yükseklikle ikiye bölündüğünde ABH ve ACH (30° 60° 90°) üçgenleri elde edilir
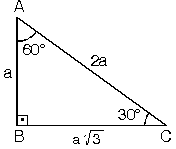



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir




45 45 90 Ucgeni Ve Ozellikleri Not Bu
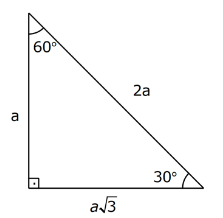
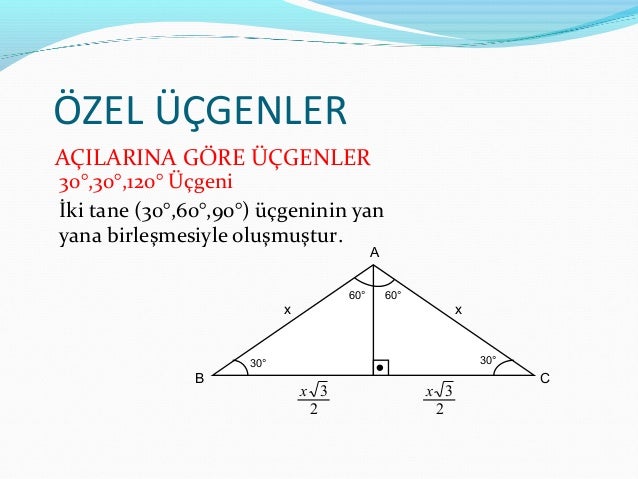
(30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar aÖ 3 olur 6 (15° 75° 90°) Üçgeni 30 60 90 üçgen, iç açıları 30°, 60° ve 90° ölçen özel bir dik üçgendir Bu özel form sayesinde, bunlardan birini biliyorsanız, diğer boyutları hesaplamak kolaydır!üçgeninin kenarları arasındaki oranların ispatını öğrenin If you're seeing this message, it means we're having trouble loading external resources on our website Bağlandığınız bilgisayar bir web filtresi kullanıyorsa, *kastaticorg ve *kasandboxorg



Ozel Ucgenler Konu Anlatimi




30 60 90 Ucgeninde 60in Karsisi 3kok2 Ise 90in Karsisi Ve 30un Karsisini Nasil Buluruz Eodev Com
30°'nin karşısındaki kenar hipotenüsün yarısına eşittir 60° nin karşısındaki kenar, 30° nin karşısındaki kenarın Ö3 katıdır 5A) 3 B) 2 C) 2 2 D) 2 3 E) 4 Çözüm 135 'lik açının olduğu yerden, dışarıya doğru bir dik üçgen oluşturursak 45 – 45 – 90 üçgeni oluşur Bu üçgenin kenarları 6'şar cm olur Büyük üçgen de 6 8 10 üçgeni olduğundan;Üçgenin dik kenarları birbirine eşit ve hipotenüsü dik kenarların katıdır Oran aşağıdaki gibidir İspatı ise çok basittir Bir dik kenara 1 cm denilirse, ikizkenarlıktan dolayı diğer dik kenar da 1 cm olmak zorundadır Pisagor Teoremi'nden de hipotenüs çıkar Üçgeni üçgeni




30 60 90 Ucgeni Matematik Geometri Ve Turkce Blogu Dgs Ales Kpss




Net Fikir Acilarina Gore Ozel Dik Ucgenler
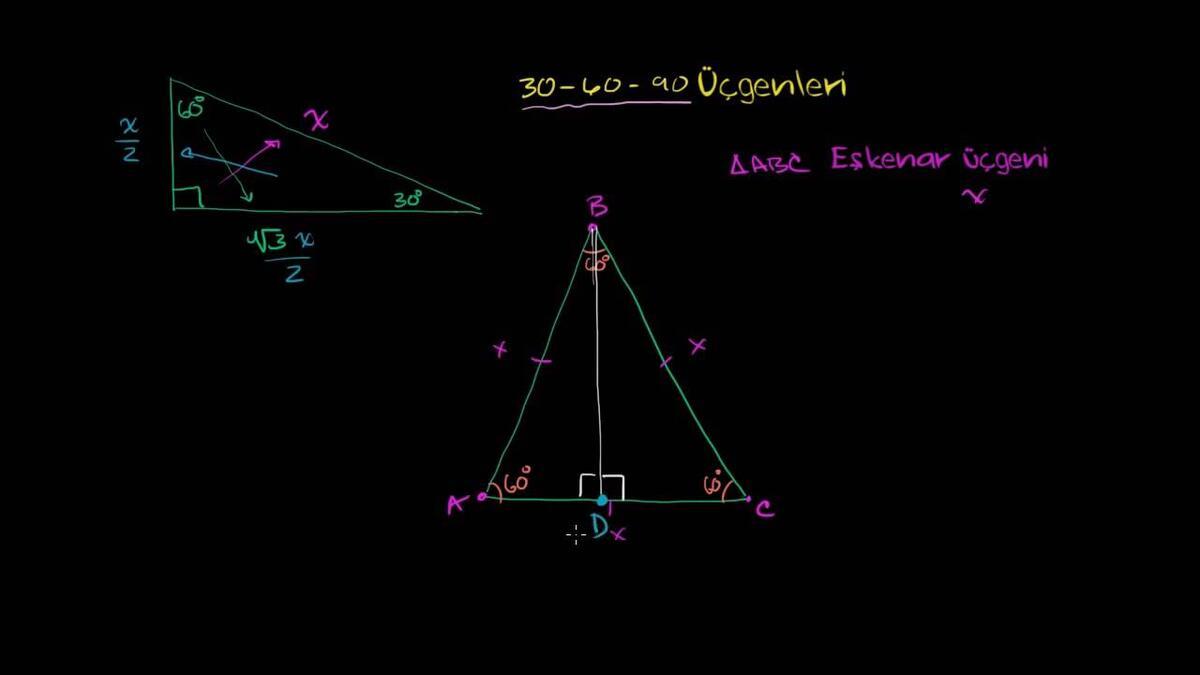
30 60 90 üçgeni kuralı bir dik üçgen üzerinden ele alınan sabit bir üçgendir 30 derecenin karşısında olan kenar hipotenüs uzunluğunun yarısına verir 60 derecenin karşısında olan kenar ise, 30 derecenin gördüğü kenar üzerinden kök 3 ile çarpılırDaha fazlası için http//wwwkhanacademyorgtrMatematikten sanat tarihine, ekonomiden fen bilimlerine, basit toplamadan diferansiyel denklemlere, ilkokul s Eşkenar üçgeninde dikme indirildiğinde 30 60 90 üçgeni elde edilir Bu oranlara göre yükseliği bulabiliriz Eşkenar üçgenin kenarlarına a dersek ve buna göre diğer kenarları oranlarsak alan formülünü elde edebiliriz Çünkü bütün üçgenlerde taban uzunluğu x yükseklik /



45 45 90 Ucgeni Matematikce



30 60 90 Ucgeni Kurali Nedir 30 60 90 Ucgeninin Ozellikleri Nelerdir Egitim Haberleri
30°'nin karşısındaki kenarhipotenüsün yarısına eşittir 60° nin karşısındaki kenar,30° nin karşısındaki kenarın Ö3 katıdır 5 (30° – 30° – 1°) Üçgeni (30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının üçgeni bir ikizkenar dik üçgendir Üçgenin dik kenarları birbirine eşit ve hipotenüsü dik kenarların katıdır Oran aşağıdaki gibidir İspatı ise çok basittir Bir dik kenara 1 cm denilirse, ikizkenarlıktan dolayı diğer dik kenar da 1 cm olmak zorundadır Pisagor Teoremi'nden de hipotenüs çıkar30, 60 ve 90 derecelik açılara sahip bir üçgen, tanım gereği sağ üçgendir, çünkü açılardan biri 90 derecedir (dik açı) Bu tip üçgenler trigonometri öğretiminde çok önemlidir, bu yüzden bu üçgenlerden birinin kenarlarının uzunluklarını ve nasıl elde edilebileceklerini bilmek önemlidir




En Hizli 30 60 90 Ucgeni Kenarlari



30 60 90 Ucgeni Pow Bylge
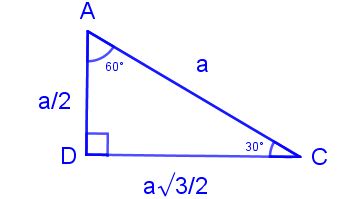
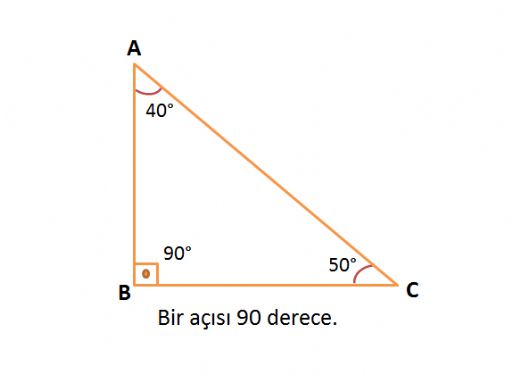
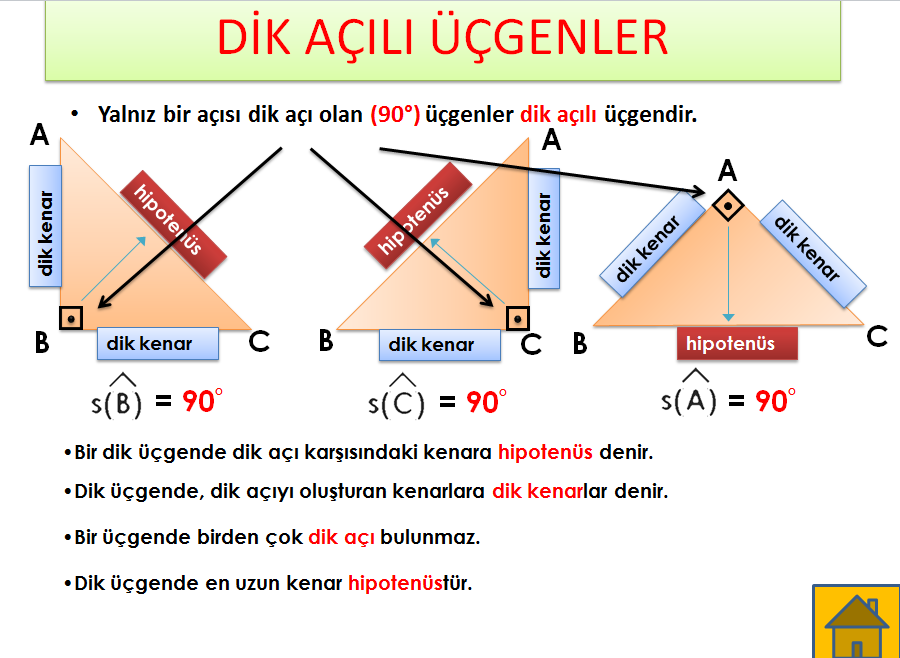
(30° – 60° – 90°) dik üçgeninde;(30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar aÖ3 olur 6 (15° 75° 90°) Üçgeni Özel Üçgenler Nelerdir, Özel Üçgenler konu anlatımı Bir açısının ölçüsü 90° olan üçgene dik üçgen denir Dik üçgende 90° nin karşısındaki kenara hipotenüs, diğer kenarlara dik kenar adı verilir Hipotenüs üçgenin daima en uzun kenarıdır şekilde, m (A) = 90° dik kenarlardır



Ozel Ucgenler Dik Ucgen Ppt Indir




Dik Ucgenler Pisagor Teoremi Konu Anlatimi Soru Cozumleri Ders Notu 9 Sinif Matematik Tyt
(30° 60° 90°) dik üçgeninde; Özel Üçgenler (), (), () ve diğerlerinin konu anlatımlarını bulabilirsiniz Üçgeni Bir dik üçgenin dik kenarları 5 ve 12 ya da bunların katları olduğu Açıları olan bir dik üçgende hipotenüs, 30°'nin karşısındaki kenar ve 60°'nin karşısındaki kenar arasında sırasıyla aşağıdaki oran vardır 30°'nin karşısındaki kenarın




Hipotenusu Verilen 30 60 90 Derece Dik Ucgeni Cizme Ortaokul Matematik



Ozel Ucgenler
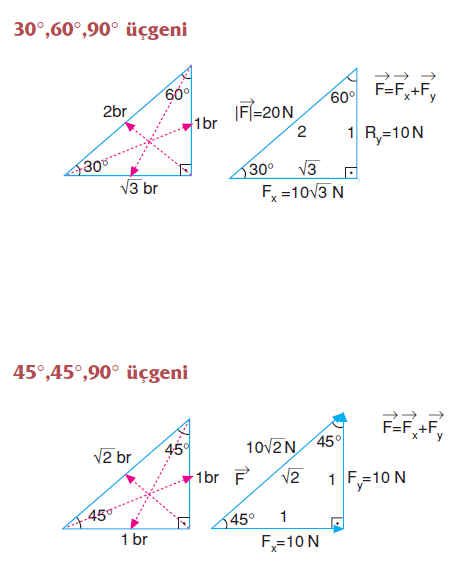
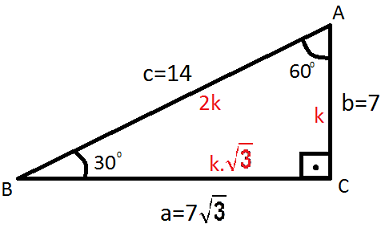
(30 60 90) Üçgeni (30 60 90) Üçgeni konusunu önce anlatıyoruz hemen ardından etkileşime geçmesini sağlıyoruz Bu şekilde kalıcılığı ve öğrenmeyi sağlıyoruz 30 60 90 üçgeni dik üçgen sınıfında bir özel üçgendir Burada 30 derecenin karşısı 1 birim, 60 derecenin karşısı √3 birim, 90 derecenin karşısı olan en uzun kenar ya da hipotenüs ise 2 birim olur Yukarıda örnek bir 30 60 90 üçgeni verilmiştir Bu üçgene iyi bakmalıyız ki özellikleri aklımızda tutalım 30 6030°'nin karşısındaki kenar hipotenüsün yarısına eşittir 60° nin karşısındaki kenar, 30° nin karşısındaki kenarın Ö3 katıdır 5




5 Soru 30 60 90 Ucgeni Youtube




30 60 90 Ucgeni Youtube
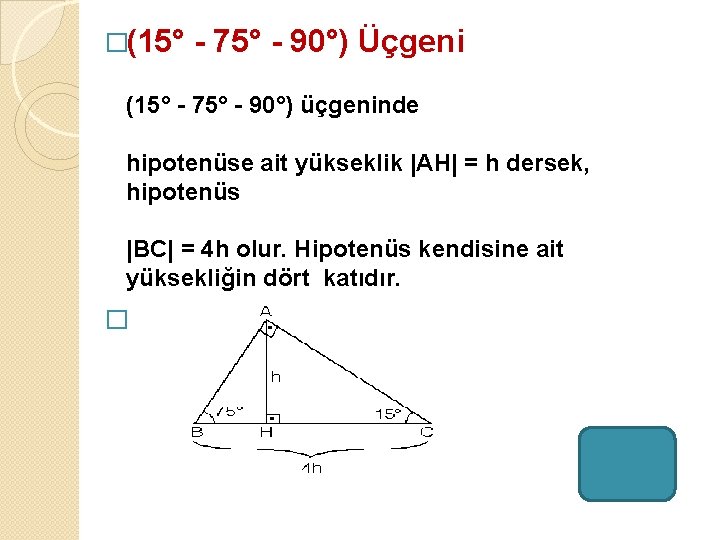
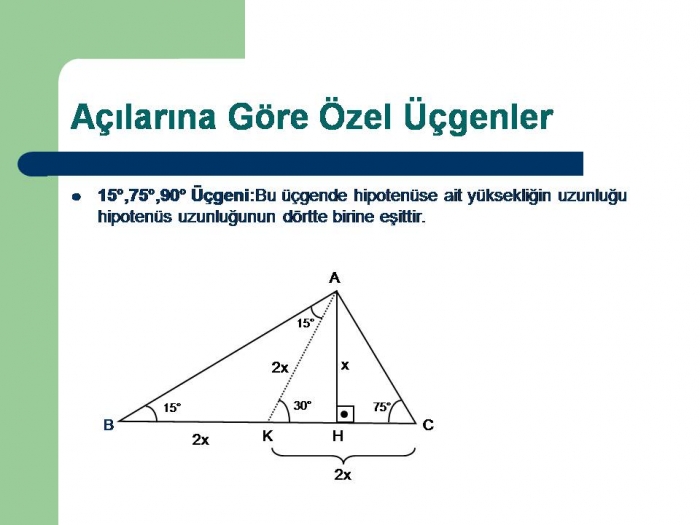
Ve bu da ikinci üçgeni BED üçgenin açılarını, dik üçgen olmasa bile, kendiniz bulabilirsiniz üçgenlerinde verilenleri kullanarak mesela üçgenin sadece bir kenarını bilsek bile diğer kenarları bulabiliyoruz(30° – 60° – 90°) dik üçgeninde;90°) üçgeni Eşkenar üçgenin yarısı olan bu üçgende, 30° nin karşısındaki kenarın uzunluğu hipotenüs uzunluğunun yarısı ve 60° nin karşısındaki kenarın uzunluğu 30° nin karşısındaki kenarın uzunluğunun 3 katıdır




Trigonometri Diyot Net Nedir




75 15 90 Ucgeni Acilarina Gore Ozel Dik Ucgenler
30 60 90 üçgeni Geometrinin açılar konusunun belirli kurallara bağlı olan özel üçgenlerinden birisidir 30 60 90 üçgeni özelliklerinin bilinmesi geometrinin temel kurallarındandır Geometri dersi bir bisikletin zinciri gibidir Dişlisinden birisi dahi çıkan b30 – 60 – 90 ÜÇGENİ Eşkenar üçgende bir kenara ait yükseklik çizilirse oluşan iki dik üçgenin de açıları 30° – 60° – 90° olur Bu eşkenar üçgenin bir kenarının uzunluğunu 2a kabul edersek, oluşan dik üçgenlerde 30 derecelik açının karşısı a olur çünkü yükseklik aynı zamanda kenarortaydır• Tüm kenarları birbirine eşittir • Tüm iç ve dış açıları birbirine eşittir Her bir iç açısı 60°, her bir dış açısı 1° dir • Bir eşkenar üçgende yükseklik çizilirse, iki tane 30° 60° 90° üçgeni oluşur • Eşkenar üçgendeki yükseklik, hem kenarortay hemde açıortaydır
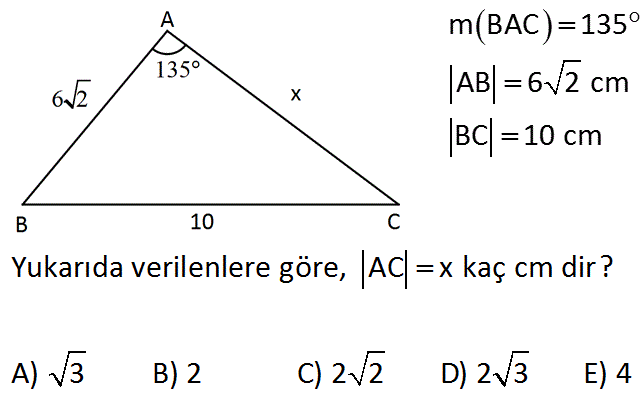



45 45 90 Ucgeni Ikizkenar Dik Ucgen



Dik Acili Ucgen Kenarlarina Gore Ucgenler
üçgeni üçgeni ve ispatı Kenarları 2 cm olan bir eşkenar üçgende köşeden indirilen dikme kenarı iki eş parçaya bölecektir Aynı zamanda da açıortay olacaktır Kenarortay olduğu için oluşan dik üçgenin alt dik kenarı 1 cm olacaktır Açıortay olduğu için de dik üçgenin bir açısı 30 √70以上 75 15 90 üçgeni kenarları 75 90 üçgeninin kenar uzunlukları 8月 31, 21 1526 Hipotenüs Uzunluğu 108,1666 birim Komşu Kenar Uzunluğu 90 birim Karşı Kenar Uzunluğu 60,0001 birim Yukarıdaki ölçüleri bildiğimizi varsayalım Aşağıdaki α ve β açısının matematiksel hesaplama formülü nedirGeometride üç farklı özel üçgen bulunmaktadır




Ozel Ucgenler Konu Anlatimi Ogretmen Tercihim




30 60 90 Ucgeni Ispat Youtube
30°'nin karşısındaki kenar hipotenüsün yarısına eşittir 60° üçgeni aynı zamanda kenarlarını da etkilemektedir Böylece açıların karşısındaki kenar ile beraber diğer kenarları üzerinden belli bir bağıntı bulunurEŞKENAR DÖRTGEN KONU NOTLARI wwwmatematikkolaynet Tüm kenarları eşit olan paralelkenara denir eşkenar dörtgen Örnek Çözüm Eşkenar dörtgen, paralelkenara ait tüm özellikleri taşıdığı için karşılıklı açıları eşit olacaktır Yani D açısı 60 dir Burada bir 30 – 60 – 90 üçgeni



Ozel Dik Ucgenler Delinetciler Portal



30 60 90 Ucgeni Pisagormatik
30°'nin karşısındaki kenar hipotenüsün yarısına eşittir 60° nin karşısındaki kenar, 30° nin karşısındaki kenarın Ö3 katıdır 5 (30° 30° 1°) Üçgeni (30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1°Bir önceki videoda üçgeninin kenar oranlarını gördük En uzun kenara x dediğimizde en kısa kenar x bölü 2 olur dedik ve aradaki kenar da yani 60 derecenin karşısındaki kenar da kök 3 çarpı x bölü 2'dir Yada şöyle de düşünebiliriz En kısa kenar 1 ise şimdi önce en kısa, sonra orta ve en uzun kenarı söyleyelimÜçgeni *İç açıları her zaman 30 60 ve 90 olan üçgenlerdir *30 derecenin karşısındaki kenar uzunluğu hipotenüsün yarısına eşittir *60 derecenin karşısındaki kenar uzunluğu ise hipotenüse eşittir Yani 30 derecenin karşısındaki kenar uzunluğunun iki katıdır




Hipotenus Uzunlugunun Belirlenmesi Tavsiyeleri September 21



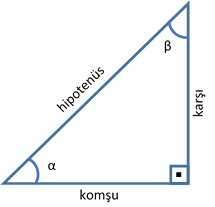
Dik Ucgende Trigonometrik Oranlar
(30° 60° 90°) dik üçgeninde;X 2 cm buluruz 11 Bu sayede üçgenden özel bir üçgen türü olan üçgeni elde edilmektedir Tüm geometrik şekillerde olduğu gibi eşkenar üçgenin de alanının da bir formülü bulunmaktadır Üçgenin alanı taban uzunluğu ile yüksekliğin çarpılması ve sonucunun ikiye



En Hizli 30 60 90 Ucgeninin Kenarlari




Ucgenler Dik Ucgenler 4 30 60 90 Ucgeni Geometri Metin Hocam Youtube




30 60 90 Ucgeni Ibrahim Hocca



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir




Ozel Acili Ucgenler Ucgeni Ozellik 30 Un Gordugu A Ise 90 In Gordugu 2a Dir 30 Un Gordugu A Ise 60 In Gordugu Ppt Indir



En Hizli 30 60 90 Ucgen Kenarlari




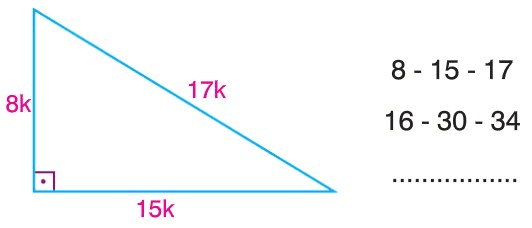
Ozel Ucgenler Nelerdir Ozel Ucgenler 8 15 17 7 24 25 30 60 90 Ve Diger Hepsi Konu Anlatimi




Mr Pen Architectural Ucgen Cetvel Seti 30 5 Cm Ucgen Olcek 11 Inc 30 60 Ve 8 Inc 45 90 Ucgen Amazon Com Tr Ofis Ve Kirtasiye



Dik Ucgende Trigonometrik Oranlar Sanatsal Egitim




15 75 90 Ucgeni Not Bu
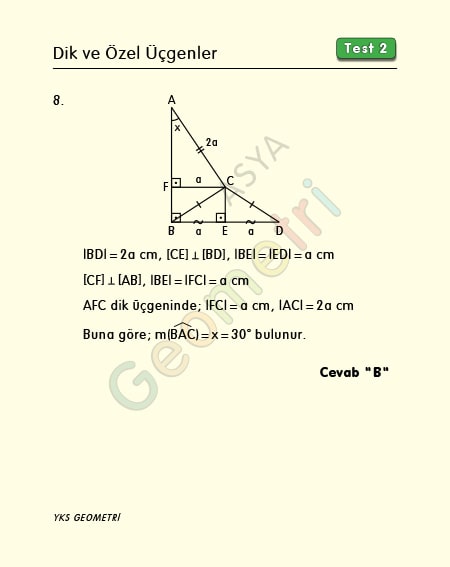



Vertical And Special Triangles Test 2 Course Geometry




Ozel Dik Ucgenler Tekrar Makale Khan Academy



Ozel Dik Ucgenler Sanatsal Egitim




Dik Ucgen Oklid Bagintisi 30 60 90 Ucgeni Kurali




Eskenar Ucgenin Alan Formulunun Ispati Ve 30 60 90 Ucgeni Youtube




Trigonometri Dik Ucgenlerdeki Trigonometrik Oranlar Matematikciler Com




30 60 90 Ucgeni




Trigonometri 30 60 90 Ve 45 45 90 Ucgenleri Ile Trigonometrik Oranlari Youtube




En Hizli 30 60 90 Ucgeni Kenar




30 60 90 Ucgeni Nedir Ozellikleri Nelerdir Nasil Hesaplanir En Son Haberler Milliyet




30 60 90 Ucgeni Turleri Ve Ozellikleri




30 60 90 Ucgeni Akilli Geometri
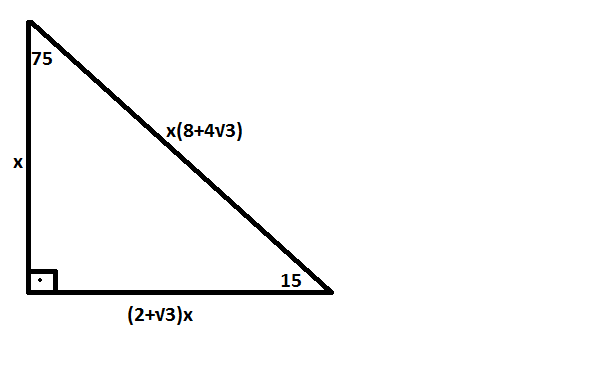



15 75 90 Ucgeni Uludag Sozluk




Ozel Ucgenler Ders Notu Konu Anlatimi Ders Notu




Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz



Teog Trigonometri Ozel Ucgenler Konu Anlatim Video Ozancorumlu Com Turkiye Nin Egitim Sitesi




15 75 90 Ucgeni Ucgende Acilar Ders Notlari Kunduz




30 60 90 Ucgeni Kurali Nedir 30 60 90 Ozel Ucgeni Ozellikleri Ve Ornek Sorular Son Dakika Egitim Haberleri




Ppt Ozel Ucgenler Powerpoint Presentation Free Download Id




En Hizli 30 60 90 Ucgeninin Ozelligi




30 60 90 Formulas Mathematics Formula



2




Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz




Ucgenler Ucgenler Ve Cesitleri




15 75 90 Ucgeni Pow Bylge
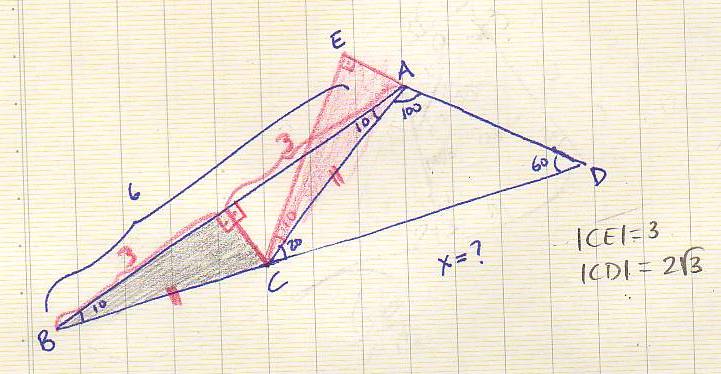



Geometri Sorusu Donanimhaber Forum




15 75 90 Ucgeni Ozellikleri Ve Kurali Soru List



45 45 90 Ucgeni Turleri Ve Ozellikleri



En Hizli 30 60 90 Ucgeni Ozellikleri



最新 75 15 90 Ucgeni シモネタ




Dik Ucgen Wikiwand




Hipotenusun Uzunlugunu Bulmanin 3 Yolu Ansiklopedi 21



En Hizli 30 60 90 Ucgenin Kenar Uzunluklari



Eskenar Ucgen Konu Anlatimi Ders Notu 9 Sinif Matematik Tyt



15 75 90 Ucgeni 2 3 Ispat



Zel Genler 1 Dk Gen 2 Kzkenar Gen




Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz



15 75 90 Ucgeni Uludag Sozluk




15 75 90 Ucgeni Webders Net



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir




30 60 90 Ucgeni Ve Ozellikleri Not Bu



90 60 30 Ucgeni



Zel Genler Dik Gen Zel Genler L L




Ucgen Nasil Hesaplanir 30 60 90 Bilim 21



Ozel Ucgenler Cozumlu Sorular Bymutlu Com




Ispat 30 60 90 Ucgeninde Kenarlarla Acilar Arasindaki Iliski Tyt Geometri Ozel Ucgenler Youtube




En Hizli 30 60 90 Ucgeninin Kenar Uzunluklari




Dik Ucgen 15 45 45 90 Ucgeni Evde Egitim Ders Calisma Ipuclari Matematik




15 75 90 Ucgen Ozelligi Ve 5 Ornek Cozum Youtube



Ppt Ozel Ucgenler Powerpoint Presentation Free Download Id




Dik Ucgen 6 15 75 90 Ucgeni Geometri Metin Hocam Youtube




22 5 67 5 90 Ucgeni Konu Anlatimi Ve Ozellikleri Eodev Com




Hipotenus Nasil Bulunur Wikihow




Hipotenus Nasil Bulunur Wikihow



Dik Ucgende Trigonometrik Hesaplamalar




30 60 90 Ucgeni Ile Ilgili Soru Lutfen Cozumlu Olsun Eodev Com



Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz




Ozel Dik Ucgenler Tekrar Makale Khan Academy




Dik Ucgen 16 15 75 90 Ucgeni Matematik Felsefesi Temel Matematik Evde Egitim



45 45 90 Ucgeni Matematikce




Ozel Ucgenler




Eskenar Ucgen Alani Not Bu




En Hizli 30 60 90 Ucgeni Kenar Uzunluklari Hesaplama
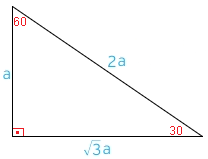



30 60 90 Ucgeni Webders Net



0 件のコメント:
コメントを投稿